Creating and Manipulating Drafting Primitives

DRAW Reference Manual

2D Drafting : 2D Drafting Primitives : Creating and Manipulating Drafting Primitives - Common Operations

Creating and Manipulating Drafting Primitives - Common Operations

Note:

Refer to Graphical Feedback for further information about creating drafting primitives.

Creating Primitives and Varying Basic Attributes

At NOTE (or VNOT) level, and with a Sheet (or VIEW Layer) in a SHOWn form, the simplest way of creating a circle (for example) would be by giving the commands:

NEW CIRCLE DEF @

The cursor would then be used to mark the centre and a circumference point of the circle, which would then be drawn. Hitting a key produces a command line giving the (Sheet) coordinates of the cursor position; such a command line could, of course, be typed in directly.) All the different shapes can be created in a similar way, with a self-explanatory prompt being output in each case.

Note:

Macros driven from forms and menus are particularly useful for 2D drafting.

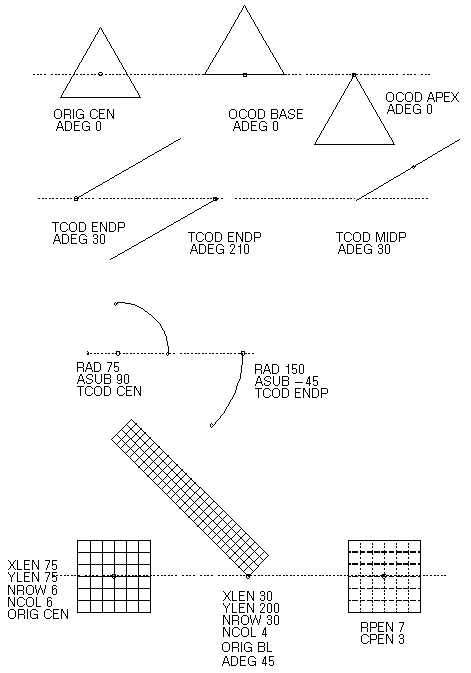
Attributes common to all primitives (except Markers, Lines, Arcs and Outlines) are orientation (ADEG, relative to a line drawn through the shape’s origin parallel to the x-axis) and origin code (OCOD). The origin code determines the position of a primitive’s origin relative to the primitive itself - for example, a circle’s origin may be placed at its centre or on its circumference. Arcs and Straight Lines have a TCOD (Type Code) attribute instead of OCOD. TCOD can be set to the endpoint or midpoint of a line, and to the endpoint or centre of an arc. The TCOD setting defines how to interpret the other attributes of the primitive. Straight lines also have an ADEG attribute. Refer to STRA and ARC elements.

Clearly, attributes such as orientation cannot be set using the cursor, so if these require settings other than their defaults they must be set afterwards. (Default orientation is 0 and default origin code is CENTRE. For straights and arcs the default TCODE is ENDPOINT.)

Alternatively, primitives may be created using one-line commands such as:

NEW CIRC RAD 50 ORIG CIRCUM ADEG 45 AT X900 Y750
NEW RECT XLEN 40 YLEN 20 ANG 45 ORIG CORNER AT @
NEW TABL XLEN 60 YLEN 60 NROW 10 NCOL 5 RPEN 2 CPEN 3
ORIG TS ADEG 45 AT @

The effects of varying the attributes of the different primitives are illustrated in Figure 17:4.: Drafting Primitives - Varying Attributes and Figure 17:5.: Drafting Primitives - Varying Attributes (continued).

Figure 17:4.

Drafting Primitives - Varying Attributes

Figure 17:5.

Drafting Primitives - Varying Attributes (continued)

Shifting the Origin

The origin code may be set in two ways. If the ORIG keyword is used (for example, ORIG @ to set by cursor), the Sheet coordinates of the origin change such that the origin moves to the specified part of the primitive - the primitive itself does not move. The origin code may also be changed by the OCOD keyword, for example

OCOD CEN
OCOD @

In this case the Sheet coordinates of the origin remain unchanged and the primitive moves so as to place itself correctly according to the new origin code.

In either case the origin position may be changed at the same time by using commands such as

ORIG X300 Y250
OCOD TRIGHT @
OCOD BLEFT @

The origin is normally invisible, but may be made visible by the SKETCH command:


SKETCH ORIGIN	At primitive level, displays primitive origin
SKETCH ORIGIN ALL	At NOTE level, displays origins of all member primitives

The command

ERASE ORIG

erases the display of the origin(s).

Moving Individual Primitives

Primitives may be moved using commands such as


AT @ AT X300 Y250	Move to new 2D position
POS ID @ POS W5500 N12345 D1200	Move to new 3D position (VNOT members only)
ON ID @ ON IDP @ ON /PUMP1 ON P1 OF /PUMP2/NS	Move to specified element origin or p-point (VNOT members only)
BY @ BY X10.5	Move relative to current 2D position
BY N500 W1200	Move relative to current 3D position (VNOT members only)

Moving Groups of Primitives

The DRAG command is used to move a group of primitives that share a common drafting point. The concentric circles are an example of a group of primitives that use the default drafting point - the drafting point’s position is not specified explicitly, so it is taken as at that of the last-created primitive. Refer to 2D Drafting Primitives for further information.


ORIGIN node_identifier	or	FPT node_identifier

Examples of the DRAG command (showing examples of node_identifier) are:

DRAG BY @
DRAG BY X120 Y-45
DRAG BY S3500 D500

DRAG TO @
DRAG TO POS @
DRAG TO IDP @
DRAG TO X120 Y-45
DRAG TO S3500 D500
DRAG TO P1 OF /VESS2/N6

FPT DRAG TO @

(The above DRAG operations have similar interpretations to the AT/ON/BY/POS commands listed previously.)

Querying Primitives

The primitives with drafting points in common with the current element may be queried by giving the command

Q COMMON

This lists the primitives that will be dragged with the current element. The primitives that may be dragged with any named drafting node of a STRAIGHT or an ARC may be queried by

Q node_id COMMON

where node-id is the FPT or TPT (etc) of a STRAIGHT or ARC.

The origin and position of a primitive may be queried by

Q ORIG

The offset of a drafting node or primitive origin from the note origin may be set and queried:

Q node_id OFFSET
Q OFFSET
node_id OFFSET X value Y value
ORIGIN OFFSET X value Y value

where node_id is the node of a straight or arc primitive, i.e. FPT, TPT, MPT, THPT or CPT. (Refer to list of DRAG commands above for examples of node_id.)

The principal dimensional and positional attributes of a primitive may be listed by using the

Q DESC

command at the primitive concerned (or at the owning View Note (position and angle)).

A drafting point on a STRAIGHT, ARC or span of an OUTLINE may be queried using

Q IDNN @

This allows you to pick one of these points by picking an appropriate position on the primitive. The query reports the appropriate point, the identity of the primitive picked and the position of the picked point. For example:

FPT OF /STRAIGHT3 X 123 Y 456
TPT OF /ARC1 E 3000 N 4000 U 0
VPT /VERT1 NEAR /VERT2 X 495 Y200

In the last case where a span of an OUTLINE was picked, the first vertex identified is the endpoint of the span, and the second is the Vertex (VRTX element) that owns the span. The two Vertex identifiers may be the same.

For STRAIGHTS and ARCS, the point identified will be the same as that returned by the Q IDN @ command where the current element is a STRA or ARC. Q IDNN @ allows both the point and the primitive to be picked by one cursor hit.

The database reference ID and the cursor-hit position of any linear element on the Sheet (for example a STRA, side of a RECT, part of Design item, etc) may be queried using:

Q IDLINE @

The query returns the database of the picked element (DRAW or DESIGN), the identity of the element, the pair of 2D coordinates that define the linear element, and the 2D position of the cursor hit.

For example, if the query were applied to a STRA element with FPT X100 Y100 and TPT X200 Y200, the following could be returned:

DRA =151/4636 LINE X 100mm Y 100mm X 200mm Y 200mm
QUAL X 167mm Y 166mm

If the query were applied to a part of a Design element, the following could be returned:

DES =35/222 LINE X 6.5/16 Y 7.19/32 X 5.3/32 Y 7.19/32
QUAL X 6.1/32 Y 7.19/32

Handling Common Drafting Primitives

When the DRAG command is used on a specified drafting primitive, this causes its drafting points to move. Other primitives that use the same drafting points will also change position. (Straights and Arcs may also change in shape.) These primitives are the common drafting primitives for specified primitive.

In order to help predict the effect that a DRAG command will have, the common drafting primitives may be highlighted or queried. The basic syntax is as follows:

HIGhlight [prim_id] COMmon
Query COMmon- at a primitive

where prim_id identifies a drafting primitive. If prim_id is omitted, the common primitives for the current element are highlighted/queried.

The DRAG command may also be used on an individual node of a Straight or Arc. The common primitives of a node may be highlighted or queried, using the following syntax:

HIGhlight prim_id COMmon prim_id


Query node_id COMmon	At a primitive At a primitive
Query COMmon node_id

For a Straight these are FPT (‘from’ point), TPT (‘to’ point) or MPT (midpoint); and for an Arc these are FPT, TPT, CPT (centre point) or THPT (‘through’ point).

The node must be currently used by the Straight or Arc. A Straight has a single node, MPT or two nodes, FPT and TPT. An Arc has an FPT, TPT and either a CPT or a THPT. If an unset node or an illegal node is specified, then an error is output.

Moving all Primitives in a NOTE or VNOT

Moving all of the member primitives of a NOTE or VNOT is done simply by changing the NOTE/VNOT’s origin position (XYPO attribute). This is the offset of the origin from the origin of the NOTE/VNOT’s owner (i.e. SHEE/VIEW respectively). The origin of a SHEE is at its bottom left-hand corner and that of a VIEW at the centre of the VIEW rectangle. XYPO may be changed directly or by the OFFSET command, for example

OFFSET X50 Y50

position NOTE VNOT’s origin at given offset owner’s origin

AT @
AT X400 Y400

position NOTE/VNOT’s origin at given position on SHEE

BY @
BY X60 Y-20

shift NOTE/VNOT’s origin by given amount

ADEG 30

rotate NOTE to 30° from horizontal

Note:

If a VNOT is moved or rotated, only primitives positioned in 2D will move with it. The positions of primitives positioned in 3D or on Design elements will remain unchanged.

Rotating a Primitive

A primitive of type ARC, CIRC, STRA, ELLI, RECT, HEXA, TABL, DMND, ETRI, OUTL or MRKP can be rotated using the ROTATE command to specify an angle of rotation and a point to rotate about. Any position reference may be used to specify the rotation point. For example:

ROTATE 45 @

Use cursor to specify the 2D point to rotate it about

ROTATE 45 IDP@

Use cursor to specify the Design p-point to rotate about

Mirroring a Primitive

A primitive of type ARC, CIRC, STRA, ELLI, RECT, HEXA, TABL, DMND, ETRI, OUTL or MRKP can be mirrored using the MIRROR command to specify a mirror axis. The current element may be mirrored in an existing linear element or two independent points may be specified to define the mirror axis. In the latter case, any position reference may be used to specify the axis points. For example:

MIRROR IN @

Use cursor to specify existing linear element to mirror in

MIRROR ABOUT @ @

Use cursor to specify two points to define mirror axis

Copying a Primitive

Copying a primitive to another position or series of positions is done by using the REPEAT command with the primitive you wish to copy as current element. The REPEAT command has three syntax variations, illustrated by the following examples:

REPEAT 5 BY X20 Y20

Produce five copies of the current primitive, each displaced (X20, Y20) from the last

REPEAT 5 BY @

Produce five copies of the current primitive, using the cursor to define displacement

REPEAT 5 @

Produce five copies of the current primitive, but with first copy at cursor position, displacement of second and subsequent copies equal to that of first copy from original

REPEAT @

Produce five copies of the current primitive, but just one repetition

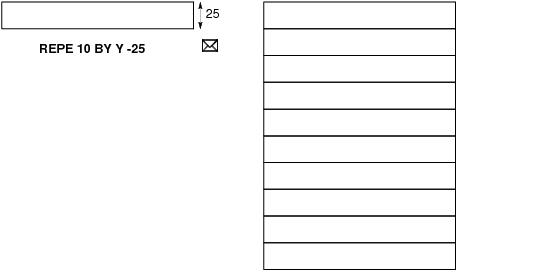
Figure 17:6.: Drafting Primitives - Use of the REPEAT Command illustrates the use of the REPEAT command.

Figure 17:6.

Drafting Primitives - Use of the REPEAT Command

Graphical Feedback

Many cursor commands generate graphical feedback (rubber banding) which makes the interaction process easy - holding down the left-hand mouse button and moving the mouse enables the primitive being created to be dragged out to the required size/orientation. Use of the commands listed below gives the Point Construction Option form, from which you can choose to define point(s) not only as simple 2D cursor hits but also as line end-points, circle centre-points, intersection points etc. The relevant commands are:


Command	Valid Elements
REGN @	VIEW
DEF @	All 2D drafting primitives
ADEF @	ARC
DIAMETER @	CIRC, HEXA
SPAN @	VRTX
RADIUS @	CIRC, HEXA, ARC
ASUB @	ARC
TPT @	STRA, ARC
FPT @	STRA, ARC
MPT @	STRA
CPT @	ARC
THPT @	ARC